Languagegenerator documentation
Table of Contents
1 Introduction
The main purpose of the LanguageGenerator class is to generate all
expressions up to a given length that are unique when evaluated on models up to
a given size. This file serves the purpose of documenting both how
LanguageGenerator achieves this conceptually, as well as its implementation.
The method that generates all the expressions up to a given length is
generate_all_sentences, which takes just the max_expression_length as an
argument: i.e. the length up to which expressions should be generated. There
are however a number of other parameters that determine the output of this
function. We define these parameters in a separate json file under
experimental_setups/ and we tell the LanguageGenerator upon initialization
which .json file to look at.
An example of such a file is
cat experiment_setups/Logical_index.json
{
"name": "Logical_index",
"number_of_subsets": 3,
"operators": [
">f",
">",
">=",
"=",
"/",
"subset",
"intersection",
"union",
"card",
"diff",
"+",
"-",
"and",
"or",
"not",
"index"
]
}
apart from the name of the experiment, there are two interesting parameters here:
- operators
- the names of the operators to be used in constructing the expressions. These names match with operators defined in src/operators.py
- number_of_subsets
- either \(3\) or \(4\). Defines a restriction on the models to be used. If \(3\), we only consider models where each element is either part of A, B or both (so only \(A\), \(B\), or \(A \cap B\)). If \(4\), also consider models where there can be elements that are not part of either (so \(A\), \(B\), or \(A \cap B\), and \(M \setminus (A \cup B)\))
So when initializing, we tell our LanguageGenerator which experiment setup to
use, by simply providing the name of the .json file:
import sys sys.path.insert(0,'..') from src.languagegenerator import LanguageGenerator lg = LanguageGenerator( max_model_size=3, experiment_setup="Logical_index", )
Let us generate all expressions up to length 6:
lg.generate_all_sentences(6)
Now before going into how the LanguageGenerator generates unique expressions up to a given length, let us describe how we represent models, expressions, and meaning of expressions.
2 Representations
2.1 Expressions
We define expressions using tuples. See some examples:
("subset", "A", ("diff", "A", ("index", "3", "B"))), ("=", "3", ("card", ("union", "A", "B"))), (">", "6", ("+", ("card", "A"), ("card", "B"))) ("+", ("card", "A"), ("card", ("index", "5", "A"))), ("card", ("index", "5", ("union", "A", "B"))), ("+", "1", ("card", ("index", "5", "A"))) ("/", ("card", "B"), ("-", ("card", "B"), "1")) ("/", ("+", "5", "6"), ("+", "2", "6")) ("/", ("card", ("index", "6", "B")), ("card", "A")) ("union", "B", ("index", "4", "A")), ("diff", ("index", "4", "A"), ("index", "6", "B")), ("index", "3", ("diff", "A", ("index", "1", "B")))
| index | 3 | (diff A (index 1 B)) |
2.2 Models
We represent models of size \(k\) here by a \(2\times k\) matrix, where the ith column
denotes the \(i^{th}\) object of the model. Each object then is represented by a
2-vector, where the first value is a 1 iff this object is in \(A\), and the
second element denotes membership of \(B\).
So for example
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
denotes a model where the first object is in \(A \cap B\), the second element is in \(B \setminus A\), the third element is in \(A \setminus B\), and the last element is in \(M \setminus (A\cup B)\).
We can equivalently represent models as a tuple of 2-tuples, where the ith 2-tuple contains the values in the \(i^{th}\) column of the matrix above. We call this the tuple format.
We define the universe up to n to be an ordered tuple/list of all models up to a size n, or simply the universe if \(n\) is clear from the context.
2.3 Representing meanings of expressions
We use a dynamic programming approach to compute the meaning of new expressions, where we combine the previously computed meanings of sub-expressions. To this end, the meaning of every expression is stored. We represent meanings of expressions in different ways, depending on the output type of the expressions. We distinguish between boolean expressions, int, float and set.
2.3.1 Boolean expressions representation
Boolean expressions are those that are either true or false on a given model. If the universe up to \(n\) is of size \(m\), then we represent a boolean expression \(e\) as a binary array of size \(m\), where the ith element is 1 iff the expression \(e\) is true on the ith model in the universe.
So an example of the meaning of a boolean expression:
lg.output_type2expression2meaning[bool][('not', ('subset', 'A', 'B'))]
| True | True | False | True | True | False | True | False | True | True | True | False | True | True | False | True | False | True | True | True | False | True | False | True | True | True | False | True | True | True | False | True | True | True | True | True | True | True | False |
2.3.2 Int and float expression representation
Expressions that evaluate to integers and floats are represented by an array the size of the universe, and the \(i^{th}\) element denotes the value of that expression for the \(i^{th}\) model:
Example of an integer meaning:
lg.output_type2expression2meaning[int][("+", ("card", "A"), ("card", "B"))]
| 1 | 1 | 2 | 2 | 2 | 3 | 2 | 3 | 2 | 3 | 3 | 4 | 3 | 3 | 4 | 3 | 4 | 3 | 4 | 4 | 5 | 3 | 4 | 3 | 4 | 4 | 5 | 3 | 4 | 4 | 5 | 3 | 4 | 4 | 5 | 4 | 5 | 5 | 6 |
2.3.3 Set representations
Representing the meaning of expressions that describe sets requires a slightly more complicated approach. Let us look at some examples:
for models_of_size in lg.output_type2expression2meaning[set]["A"]: print(models_of_size,'\n')
[[0 1 1]] [[0 0 0 1 1 1 1 1 1] [0 1 1 0 0 1 1 1 1]] [[0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1] [0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1] [0 1 1 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1]]
What we see above is 3 matrices, one for each model size. We represent A here by setting the values to 1 that represent elements that belong to A. Let us look at another example of B:
for models_of_size in lg.output_type2expression2meaning[set]["B"]: print(models_of_size, "\n")
[[1 0 1]] [[1 1 1 0 1 0 0 1 1] [1 0 1 1 1 0 1 0 1]] [[1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 0 0 1 1 0 0 0 0 1 1 1 1] [1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 0 1 0 0 1 1 0 0 1 1] [1 0 1 1 1 0 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 0 1 0 1 0 1]]
Now let us look at what the meaning of the expression \(A \cap B\) looks like:
for models_of_size in lg.output_type2expression2meaning[set][ ("intersection", "A", "B") ]: print(models_of_size, "\n")
[[0 0 1]] [[0 0 0 0 1 0 0 1 1] [0 0 1 0 0 0 1 0 1]] [[0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 1 1 0 0 0 0 1 1 1 1] [0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 1 0 1 0 0 1 1 0 0 1 1] [0 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 1 0 1 0 1]]
We can see that representing the intersection of A and B corresponds to preforming the element-wise AND operation on the set representations of A and B. For the union, we have
for models_of_size in lg.output_type2expression2meaning[set][ ("union", "A", "B") ]: print(models_of_size, "\n")
[[1 1 1]] [[1 1 1 1 1 1 1 1 1] [1 1 1 1 1 1 1 1 1]] [[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1] [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1] [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]]
exactly what we expected: all ones. This is because we only consider models where every element is at part of at least one of A or B.
3 Getting started
As shown above, we can use the LanguageGenerator by pointing it to the
experiment_setup json file to be used, and setting maximum model size:
import src from src.languagegenerator import LanguageGenerator lg = LanguageGenerator(max_model_size=3, experiment_setup="Logical_index", )
'org_babel_python_eoe'
4 How expressions are generated
We generate all expressions by starting with expressions of length 1, storing
their meanings, and then defining expressions of greater length by combining
previously formed sub-expressions. For each new expression, its meaning is
computed and only if its meaning is not the same as any previously formed
meaning, we store it as a new expression (which will be used in later
expressions as subexpressions again). The method that implements this
functionality is generate_all_sentences, which takes the length of the
expressions to be generated.
By default, the LanguageGenerator will store itself, and the expressions
generated for each length up to the given length in .dill format under the
results/ folder. The name of the folder in the results folder to be used is
uniquely identifying for the parameters that lead to generation of these
sentences, e.g. results/Experiment=Logical_index-max_model_size=5/..
Now let's see what all expressions up to length 4 look like Let's see what all unique boolean expressions up to length 4 looks like:
lg.generate_all_sentences(4)
| True | False | (subset A A) | (subset A B) | (subset B A) | (subset B B) | (> 1 (card A)) | (> 1 (card B)) | (> 2 (card A)) | (> 2 (card B)) | (> 3 (card A)) | (> 3 (card B)) | (> (card A) 1) | (> (card A) 2) | (> (card B) 1) | (> (card B) 2) | (= 1 (card A)) | (= 1 (card B)) | (= 2 (card A)) | (= 2 (card B)) | (not (subset A B)) | (not (subset B A)) |
5 Scoring
The LanguageGenerator is also able to score the expressions it has generated
based on some custom-defined signature function. See score.pdf for more
information on the scoring itself.
We define a meaning matrix to be a pd.DataFrame that is indexed by the unique
models in the universe, represented in tuple format, and where each column
corresponds to an expression:
meaning_matrix = lg.get_meaning_matrix()
meaning_matrix
True False ... (=, 1, (card, B)) (=, 1, (card, A))
((0, 1),) 1 0 ... 1 0
((1, 0),) 1 0 ... 0 1
((1, 1),) 1 0 ... 1 1
((0, 1), (0, 1)) 1 0 ... 0 0
((0, 1), (1, 0)) 1 0 ... 1 1
((0, 1), (1, 1)) 1 0 ... 0 1
((1, 0), (0, 1)) 1 0 ... 1 1
((1, 1), (0, 1)) 1 0 ... 0 1
((1, 0), (1, 0)) 1 0 ... 0 0
((1, 0), (1, 1)) 1 0 ... 1 0
((1, 1), (1, 0)) 1 0 ... 1 0
((1, 1), (1, 1)) 1 0 ... 0 0
((0, 1), (0, 1), (0, 1)) 1 0 ... 0 0
((0, 1), (0, 1), (1, 0)) 1 0 ... 0 1
((0, 1), (0, 1), (1, 1)) 1 0 ... 0 1
((0, 1), (1, 0), (0, 1)) 1 0 ... 0 1
((0, 1), (1, 1), (0, 1)) 1 0 ... 0 1
((0, 1), (1, 0), (1, 0)) 1 0 ... 1 0
((0, 1), (1, 0), (1, 1)) 1 0 ... 0 0
((0, 1), (1, 1), (1, 0)) 1 0 ... 0 0
((0, 1), (1, 1), (1, 1)) 1 0 ... 0 0
((1, 0), (0, 1), (0, 1)) 1 0 ... 0 1
((1, 1), (0, 1), (0, 1)) 1 0 ... 0 1
((1, 0), (0, 1), (1, 0)) 1 0 ... 1 0
((1, 0), (0, 1), (1, 1)) 1 0 ... 0 0
((1, 1), (0, 1), (1, 0)) 1 0 ... 0 0
((1, 1), (0, 1), (1, 1)) 1 0 ... 0 0
((1, 0), (1, 0), (0, 1)) 1 0 ... 1 0
((1, 0), (1, 1), (0, 1)) 1 0 ... 0 0
((1, 1), (1, 0), (0, 1)) 1 0 ... 0 0
((1, 1), (1, 1), (0, 1)) 1 0 ... 0 0
((1, 0), (1, 0), (1, 0)) 1 0 ... 0 0
((1, 0), (1, 0), (1, 1)) 1 0 ... 1 0
((1, 0), (1, 1), (1, 0)) 1 0 ... 1 0
((1, 0), (1, 1), (1, 1)) 1 0 ... 0 0
((1, 1), (1, 0), (1, 0)) 1 0 ... 1 0
((1, 1), (1, 0), (1, 1)) 1 0 ... 0 0
((1, 1), (1, 1), (1, 0)) 1 0 ... 0 0
((1, 1), (1, 1), (1, 1)) 1 0 ... 0 0
[39 rows x 22 columns]
The cell in position \(i \times j\) is 1 iff the \(j^{th}\) expression is true on the \(i^{th}\) model.
5.1 Signature functions
We defined signature functions for graded measures of monotonicity, quantity, and conserativity in src/signature_functions.py. As discussed in score.pdf, signature functions induce partitions on the meaning matrix. Our implementation of signature functions only take the meaning matrix, and return the induced partition.
We distinguish between expression-invariant signature functions and expression-sensitive signature functions:
A signature function is expression-invariant if it purely a function of the models itself. A signature function is expression-sensitive, on the other hand, if it's value for a particular model is expression-specific.
For instance, the signature function for quantity is expression-invariant: it simply maps each model to a tuple with information on the cardinalities of the relevant subsets of that model (\(|A|\), \(|B|\), \(|A \cap B|\), \(M \setminus (A \cup B)\)). Therefore, the results of the quantity signature look like:
from src import signature_functions signature_quantity_output = signature_functions.signature_quantity( meaning_matrix ) signature_quantity_output
((0, 1),) (0, 0, 1, 0) ((1, 0),) (0, 1, 0, 0) ((1, 1),) (1, 0, 0, 0) ((0, 1), (0, 1)) (0, 0, 2, 0) ((0, 1), (1, 0)) (0, 1, 1, 0) ((0, 1), (1, 1)) (1, 0, 1, 0) ((1, 0), (0, 1)) (0, 1, 1, 0) ((1, 1), (0, 1)) (1, 0, 1, 0) ((1, 0), (1, 0)) (0, 2, 0, 0) ((1, 0), (1, 1)) (1, 1, 0, 0) ((1, 1), (1, 0)) (1, 1, 0, 0) ((1, 1), (1, 1)) (2, 0, 0, 0) ((0, 1), (0, 1), (0, 1)) (0, 0, 3, 0) ((0, 1), (0, 1), (1, 0)) (0, 1, 2, 0) ((0, 1), (0, 1), (1, 1)) (1, 0, 2, 0) ((0, 1), (1, 0), (0, 1)) (0, 1, 2, 0) ((0, 1), (1, 1), (0, 1)) (1, 0, 2, 0) ((0, 1), (1, 0), (1, 0)) (0, 2, 1, 0) ((0, 1), (1, 0), (1, 1)) (1, 1, 1, 0) ((0, 1), (1, 1), (1, 0)) (1, 1, 1, 0) ((0, 1), (1, 1), (1, 1)) (2, 0, 1, 0) ((1, 0), (0, 1), (0, 1)) (0, 1, 2, 0) ((1, 1), (0, 1), (0, 1)) (1, 0, 2, 0) ((1, 0), (0, 1), (1, 0)) (0, 2, 1, 0) ((1, 0), (0, 1), (1, 1)) (1, 1, 1, 0) ((1, 1), (0, 1), (1, 0)) (1, 1, 1, 0) ((1, 1), (0, 1), (1, 1)) (2, 0, 1, 0) ((1, 0), (1, 0), (0, 1)) (0, 2, 1, 0) ((1, 0), (1, 1), (0, 1)) (1, 1, 1, 0) ((1, 1), (1, 0), (0, 1)) (1, 1, 1, 0) ((1, 1), (1, 1), (0, 1)) (2, 0, 1, 0) ((1, 0), (1, 0), (1, 0)) (0, 3, 0, 0) ((1, 0), (1, 0), (1, 1)) (1, 2, 0, 0) ((1, 0), (1, 1), (1, 0)) (1, 2, 0, 0) ((1, 0), (1, 1), (1, 1)) (2, 1, 0, 0) ((1, 1), (1, 0), (1, 0)) (1, 2, 0, 0) ((1, 1), (1, 0), (1, 1)) (2, 1, 0, 0) ((1, 1), (1, 1), (1, 0)) (2, 1, 0, 0) ((1, 1), (1, 1), (1, 1)) (3, 0, 0, 0) dtype: object
The signature function for monotonicity, however, is expression-sensitive, as it depends on the presence of a submodel that satisfies the expression. The output of this signature function is therefore of the same shape as the meaning matrix:
signature_monotonicity_output = signature_functions.signature_monotonicity( meaning_matrix ) signature_monotonicity_output
True False ... (=, 1, (card, B)) (=, 1, (card, A))
((0, 1),) True False ... True False
((1, 0),) True False ... True True
((1, 1),) True False ... True True
((0, 1), (0, 1)) True False ... True False
((0, 1), (1, 0)) True False ... True True
((0, 1), (1, 1)) True False ... True True
((1, 0), (0, 1)) True False ... True True
((1, 1), (0, 1)) True False ... True True
((1, 0), (1, 0)) True False ... True False
((1, 0), (1, 1)) True False ... True False
((1, 1), (1, 0)) True False ... True False
((1, 1), (1, 1)) True False ... True False
((0, 1), (0, 1), (0, 1)) True False ... True False
((0, 1), (0, 1), (1, 0)) True False ... True True
((0, 1), (0, 1), (1, 1)) True False ... True True
((0, 1), (1, 0), (0, 1)) True False ... True True
((0, 1), (1, 1), (0, 1)) True False ... True True
((0, 1), (1, 0), (1, 0)) True False ... True False
((0, 1), (1, 0), (1, 1)) True False ... True False
((0, 1), (1, 1), (1, 0)) True False ... True False
((0, 1), (1, 1), (1, 1)) True False ... True False
((1, 0), (0, 1), (0, 1)) True False ... True True
((1, 1), (0, 1), (0, 1)) True False ... True True
((1, 0), (0, 1), (1, 0)) True False ... True False
((1, 0), (0, 1), (1, 1)) True False ... True False
((1, 1), (0, 1), (1, 0)) True False ... True False
((1, 1), (0, 1), (1, 1)) True False ... True False
((1, 0), (1, 0), (0, 1)) True False ... True False
((1, 0), (1, 1), (0, 1)) True False ... True False
((1, 1), (1, 0), (0, 1)) True False ... True False
((1, 1), (1, 1), (0, 1)) True False ... True False
((1, 0), (1, 0), (1, 0)) True False ... False False
((1, 0), (1, 0), (1, 1)) True False ... True False
((1, 0), (1, 1), (1, 0)) True False ... True False
((1, 0), (1, 1), (1, 1)) True False ... True False
((1, 1), (1, 0), (1, 0)) True False ... True False
((1, 1), (1, 0), (1, 1)) True False ... True False
((1, 1), (1, 1), (1, 0)) True False ... True False
((1, 1), (1, 1), (1, 1)) True False ... True False
[39 rows x 22 columns]
A cell in position \(i \times j\) is True iff the \(i^{th}\) model has a submodel that satisfies the \(j^{th}\) expression.
5.2 Computing scores for the expressions
So while the signature function computes the induced partition, the
LanguageGenerator.get_exp2score method implements the computation of the
reduction of entropy that the provided signature function provides with
respect to knowing if a model satisfies a given expression or not. Again,
see score.pdf for more information on how this is computed.
The output of LanguageGenerator.get_exp2score is a pd.Series that is
indexed by expressions, and maps each expression to its score:
exp2score_monotonicity = lg.get_exp2score( signature_functions.signature_monotonicity ) exp2score_monotonicity
True 1.000000 False 1.000000 (subset, B, B) 0.259171 (subset, B, A) 0.260862 (subset, A, B) 1.000000 (subset, A, A) 1.000000 (not, (subset, B, A)) 0.000000 (not, (subset, A, B)) 0.000000 (>, (card, B), 2) 0.516886 (>, (card, B), 1) 0.362747 (>, (card, A), 2) 1.000000 (>, (card, A), 1) 1.000000 (>, 3, (card, B)) 0.000000 (>, 3, (card, A)) 1.000000 (>, 2, (card, B)) 0.000000 (>, 2, (card, A)) 1.000000 (>, 1, (card, B)) 0.023665 (>, 1, (card, A)) 1.000000 (=, 2, (card, B)) 0.186723 (=, 2, (card, A)) 1.000000 (=, 1, (card, B)) 0.015518 (=, 1, (card, A)) 1.000000 dtype: float64
And for conservativity:
exp2score_conservativity = lg.get_exp2score( signature_functions.signature_conservativity ) exp2score_conservativity
True 1.000000 False 1.000000 (subset, B, B) 0.531720 (subset, B, A) 0.592618 (subset, A, B) 1.000000 (subset, A, A) 1.000000 (not, (subset, B, A)) 0.592618 (not, (subset, A, B)) 1.000000 (>, (card, B), 2) 0.579694 (>, (card, B), 1) 0.489300 (>, (card, A), 2) 1.000000 (>, (card, A), 1) 1.000000 (>, 3, (card, B)) 0.579694 (>, 3, (card, A)) 1.000000 (>, 2, (card, B)) 0.489300 (>, 2, (card, A)) 1.000000 (>, 1, (card, B)) 0.531720 (>, 1, (card, A)) 1.000000 (=, 2, (card, B)) 0.369893 (=, 2, (card, A)) 1.000000 (=, 1, (card, B)) 0.369402 (=, 1, (card, A)) 1.000000 dtype: float64
Considering none of these expressions contain the index operator, we already know that all the quantity scores are going to be 1:
exp2score_quantity = lg.get_exp2score(signature_functions.signature_quantity)
exp2score_quantity
True 1.0 False 1.0 (subset, B, B) 1.0 (subset, B, A) 1.0 (subset, A, B) 1.0 (subset, A, A) 1.0 (not, (subset, B, A)) 1.0 (not, (subset, A, B)) 1.0 (>, (card, B), 2) 1.0 (>, (card, B), 1) 1.0 (>, (card, A), 2) 1.0 (>, (card, A), 1) 1.0 (>, 3, (card, B)) 1.0 (>, 3, (card, A)) 1.0 (>, 2, (card, B)) 1.0 (>, 2, (card, A)) 1.0 (>, 1, (card, B)) 1.0 (>, 1, (card, A)) 1.0 (=, 2, (card, B)) 1.0 (=, 2, (card, A)) 1.0 (=, 1, (card, B)) 1.0 (=, 1, (card, A)) 1.0 dtype: float64
5.3 Visualizing results
In addition to computing the scores, the LanguageGenerator also implements
visualizing the resulting scores as .png or as rotating .gif (in case of
3 scores).
Let's first compute expressions up to a greater length so that we can see some spread in the quantity scores as well.
import os lg = LanguageGenerator( max_model_size=3, experiment_setup="Logical_index", ) lg.generate_all_sentences(6)
['True',
'False',
('subset', 'A', 'A'),
('subset', 'A', 'B'),
('subset', 'B', 'A'),
('subset', 'B', 'B'),
('>', '1', ('card', 'A')),
('>', '1', ('card', 'B')),
('>', '2', ('card', 'A')),
('>', '2', ('card', 'B')),
('>', '3', ('card', 'A')),
('>', '3', ('card', 'B')),
('>', ('card', 'A'), '1'),
('>', ('card', 'A'), '2'),
('>', ('card', 'B'), '1'),
('>', ('card', 'B'), '2'),
('=', '1', ('card', 'A')),
('=', '1', ('card', 'B')),
('=', '2', ('card', 'A')),
('=', '2', ('card', 'B')),
('not', ('subset', 'A', 'B')),
('not', ('subset', 'B', 'A')),
('>', ('card', 'A'), ('card', 'B')),
('>', ('card', 'B'), ('card', 'A')),
('>=', ('card', 'A'), ('card', 'B')),
('>=', ('card', 'B'), ('card', 'A')),
('=', ('card', 'A'), ('card', 'B')),
('subset', 'A', ('diff', 'A', 'B')),
('subset', 'A', ('index', '0', 'B')),
('subset', 'A', ('index', '1', 'B')),
('subset', 'A', ('index', '2', 'B')),
('subset', 'A', ('index', '3', 'B')),
('subset', 'B', ('diff', 'B', 'A')),
('subset', 'B', ('index', '0', 'A')),
('subset', 'B', ('index', '1', 'A')),
('subset', 'B', ('index', '2', 'A')),
('subset', 'B', ('index', '3', 'A')),
('subset', ('intersection', 'A', 'B'), 'A'),
('subset', ('union', 'A', 'B'), 'A'),
('subset', ('union', 'A', 'B'), 'B'),
('subset', ('diff', 'A', 'B'), 'A'),
('subset', ('diff', 'B', 'A'), 'B'),
('subset', ('index', '0', 'A'), 'B'),
('subset', ('index', '0', 'B'), 'A'),
('subset', ('index', '1', 'A'), 'B'),
('subset', ('index', '1', 'B'), 'A'),
('subset', ('index', '2', 'A'), 'B'),
('subset', ('index', '2', 'B'), 'A'),
('subset', ('index', '3', 'A'), 'B'),
('subset', ('index', '3', 'B'), 'A'),
('not', ('=', '1', ('card', 'A'))),
('not', ('=', '1', ('card', 'B'))),
('not', ('=', '2', ('card', 'A'))),
('not', ('=', '2', ('card', 'B'))),
('>', '1', ('card', ('intersection', 'A', 'B'))),
('>', '1', ('card', ('index', '0', 'A'))),
('>', '1', ('card', ('index', '0', 'B'))),
('>', '2', ('card', ('intersection', 'A', 'B'))),
('>', '2', ('card', ('union', 'A', 'B'))),
('>', '2', ('card', ('diff', 'A', 'B'))),
('>', '2', ('card', ('diff', 'B', 'A'))),
('>', '3', ('card', ('intersection', 'A', 'B'))),
('>', '3', ('card', ('union', 'A', 'B'))),
('>', '3', ('card', ('diff', 'A', 'B'))),
('>', '3', ('card', ('diff', 'B', 'A'))),
('>', ('card', ('intersection', 'A', 'B')), '1'),
('>', ('card', ('intersection', 'A', 'B')), '2'),
('>', ('card', ('union', 'A', 'B')), '1'),
('>', ('card', ('union', 'A', 'B')), '2'),
('>', ('card', ('diff', 'A', 'B')), '1'),
('>', ('card', ('diff', 'A', 'B')), '2'),
('>', ('card', ('diff', 'B', 'A')), '1'),
('>', ('card', ('diff', 'B', 'A')), '2'),
('=', '1', ('card', ('intersection', 'A', 'B'))),
('=', '1', ('card', ('diff', 'A', 'B'))),
('=', '1', ('card', ('diff', 'B', 'A'))),
('=', '2', ('card', ('intersection', 'A', 'B'))),
('=', '2', ('card', ('union', 'A', 'B'))),
('=', '2', ('card', ('diff', 'A', 'B'))),
('=', '2', ('card', ('diff', 'B', 'A'))),
('subset', 'A', ('index', ('card', 'B'), 'A')),
('subset', 'A', ('index', ('card', 'B'), 'B')),
('subset', 'B', ('index', ('card', 'A'), 'A')),
('subset', ('index', ('card', 'A'), 'A'), 'B'),
('subset', ('index', ('card', 'A'), 'B'), 'A'),
('subset', ('index', ('card', 'A'), 'B'), 'B'),
('subset', ('index', ('card', 'B'), 'A'), 'A'),
('subset', ('index', ('card', 'B'), 'A'), 'B'),
('subset', ('index', ('card', 'B'), 'B'), 'A'),
('not', ('=', ('card', 'A'), ('card', 'B'))),
('not', ('subset', 'A', ('diff', 'A', 'B'))),
('not', ('subset', 'A', ('index', '0', 'B'))),
('not', ('subset', 'A', ('index', '1', 'B'))),
('not', ('subset', 'A', ('index', '2', 'B'))),
('not', ('subset', 'A', ('index', '3', 'B'))),
('not', ('subset', 'B', ('diff', 'B', 'A'))),
('not', ('subset', 'B', ('index', '0', 'A'))),
('not', ('subset', 'B', ('index', '1', 'A'))),
('not', ('subset', 'B', ('index', '2', 'A'))),
('not', ('subset', 'B', ('index', '3', 'A'))),
('not', ('subset', ('index', '1', 'A'), 'B')),
('not', ('subset', ('index', '1', 'B'), 'A')),
('not', ('subset', ('index', '2', 'A'), 'B')),
('not', ('subset', ('index', '2', 'B'), 'A')),
('not', ('subset', ('index', '3', 'A'), 'B')),
('not', ('subset', ('index', '3', 'B'), 'A'))]
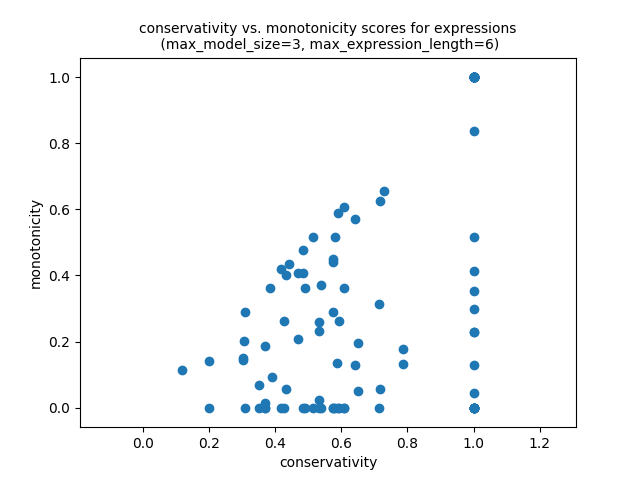
Now if we want to produce a 2d scatter plot showing the conservativity vs. monotonicity, we do:
lg.plot_png( [ signature_functions.signature_conservativity, signature_functions.signature_monotonicity, ], )
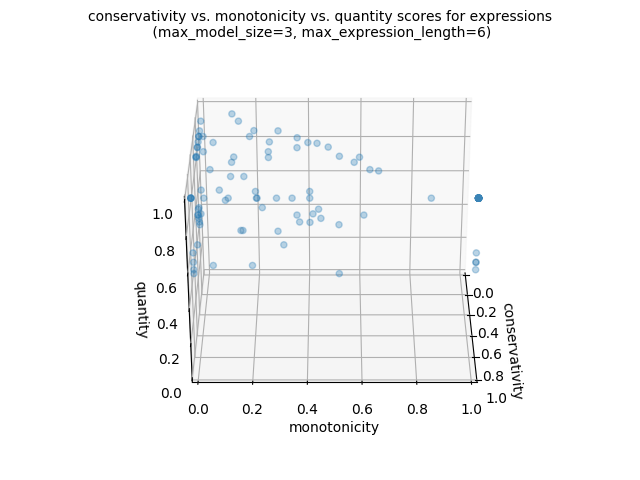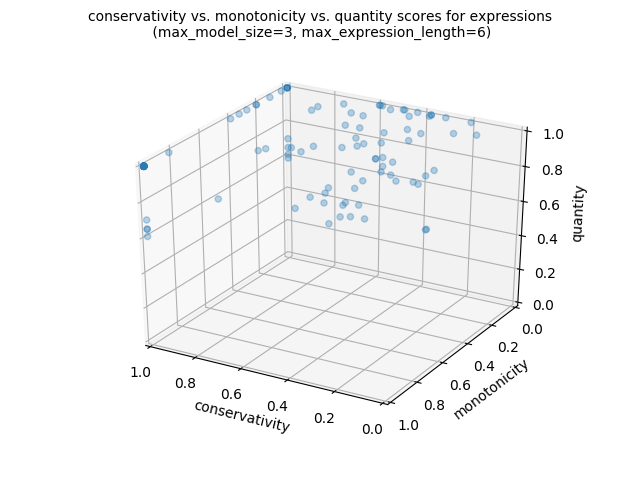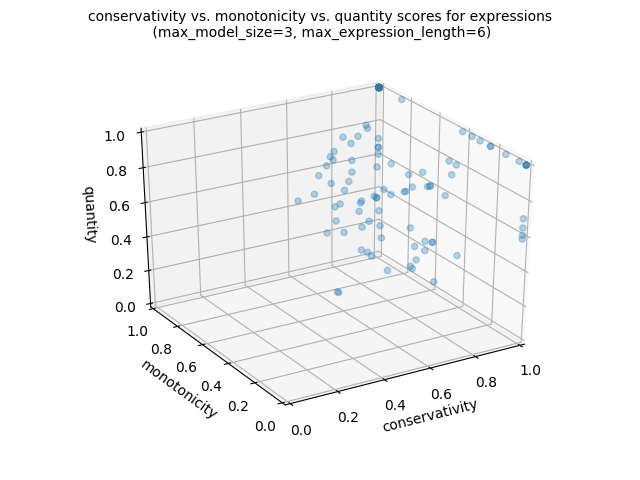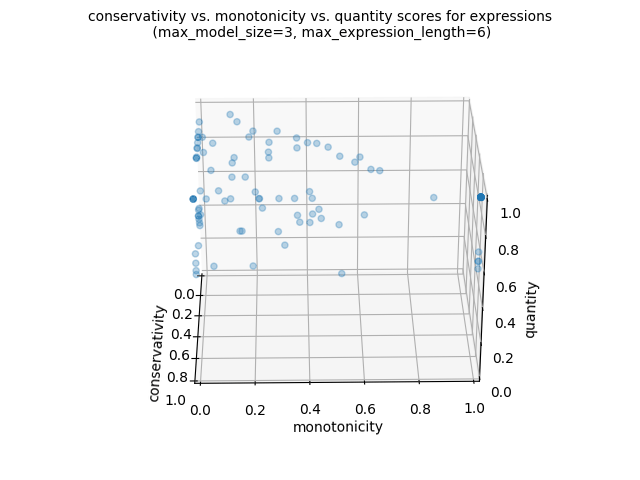
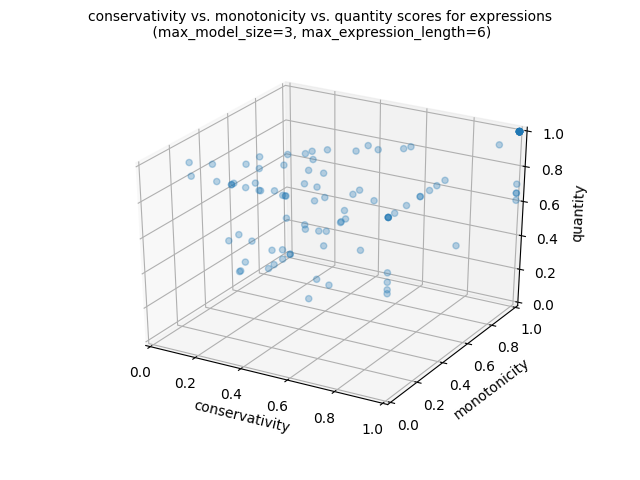
Of if we want to produce a 3d scatter plot:
import os lg.plot_png( [ signature_functions.signature_conservativity, signature_functions.signature_monotonicity, signature_functions.signature_quantity, ], )
In addition, it is possible to produce 3d scatter gifs:
lg.plot_gif( [ signature_functions.signature_conservativity, signature_functions.signature_monotonicity, signature_functions.signature_quantity, ], angle_shift_per_frame=1, frame_rate=1 / 24, )